Hyper

• info : virtual reality project for CAVE
• date : 2010
• ware : 4-wall CAVE, IS-900 tracking, Max/MSP

Hyper - make a step into the fourth dimension

Hyper creates a virtual reality environment inside a CAVE that allows visitors to engage with the potential of higher spatial dimensions. Head-tracking makes it possible to place a virtual geometric object in the center of the space. The user can physically walk around the object and/or manipulate it with a hand-held device. By exchanging axes, users are invited to step into the fourth dimension at their own pace. The intuitive interaction of Hyper gives users the opportunity to open and bend their minds in order to reach an understanding of a world beyond X-Y-Z.

Hyper Dimension

If our universe is placed on a hyperbolic sphere, then every single point in space is the exact center of the universe. And the universe is finite yet seamless, as it wraps around all the edges. I think that might just be the most elegant solution for the mystery of the universe. And all it needs is just one additional spatial dimension - the fourth. Or fifth, depending on where you start counting. The fourth spatial dimension is generally referred to as the W-dimension. It's directions (like up/down, left/right, for/back) are generally called ana/kata.

Higher dimensions are not just science fiction. In theoretical physics String theory is the first candidate to solve the theory of everything. The vibration of strings in higher dimensions explain particles and their specific charge, mass and spin. Different theories require different amounts of dimensions: M-Theory needs 11 dimensions, bosonic String theory needs even 26 dimensions. And even though those extra dimensions could be so small that it is impossible to detect them, they challenge our understanding of space to it's limits.

If you want to look at what the equivalent of a tetrahedron looks like in 7 dimensions, you will find lots of colorful and confusing images on the net. Even though some of those representations are interactive, and some are stereoscopic, i missed a more tactile, more intuitive way of perceiving those objects. Having read Rudy Rucker's The Fourth Dimension and all his thought experiments, i got inspired to create my own attempt at visualizing the fourth spatial dimension.

Grasping Hyper Dimensions

We are beings with 2-dimensional retinas. By comparing the 2D images perceived by our left and right eye our brain creates a 3-dimensional understanding of the world around us. Width, height and depth are the three spatial dimensions we are familiar with. If there were multiple dimensions around us, we wouldn't be able to perceive them as such. Objects and events happening in higher dimensions would seem illogical and mystical to us.

To be able to grasp what it means to understand a higher dimension, we need to take a step down and look at the problem from a lower dimension. Edwin Abbott's novel Flatland from 1884 tells the story of a 2-dimensional square in a 2-dimensional world that gets introduced to the third dimension. Of course A Square has trouble grasping this new extra dimension that he has never experienced, and is also not equipped to experience. He can only perceive 3-dimensional objects as their intersections when they overlap with his 2D world, or as shadow projections onto flatland.

Similarly, we use a technique to project 3D shapes down onto 2D, as most of our drawing, designing, creating happens on 2D surfaces - paper, canvases or screens. By using perspective projection and hidden line removal we learned to read these flat representations as 3D shapes. Hyper now uses a 3-dimensional space - a virtual reality cave - to try to visualize the fourth dimension. It allows the 4th dimension to be projected down into the 3rd dimension, in the same way as the 3rd dimension can be projected down into the 2nd dimension when drawing 3-dimensional objects on paper. (The ability of creating real-time interactive experiences in CAVEs obviously wins against the static 3D space of sculptures.)

The Setup

After having spent some time updating the hardware and software at the Banff New Media Institute's 5-wall passive stereo CAVE, and after creating some demo patches, I was eager to put some 4D math into it.

The CAVE has a InterSense tracking unit, a head tracker and a wand, that allows very accurate tracking of the users head position and orientation. The whole experience i created is made for only one user at a time, as the projections are custom created for the person wearing the head tracking device.

In order to give the user the freedom to walk around the CAVE space (~ 2.5*2.5m) and walk around the projected geometric shapes, it was the logical conclusion to place the virtual objects exactly in the middle of the space. Typical CAVE installation create 3-dimensional illusion that lie behind the screens. Creating a projection that is more holographic and in closer touching-distance for the user, is harder to accomplish and also more straining for the user's eyes. The quite binocular disparity values (distance between left and right image) can make you dizzy after a while.

The CAVE currently runs with Max/MSP, which allows easy prototyping of projects. Jitter allows to write your own OpenGl code in the [jit.gl.sketch] object. I created Max/MSP patches that render objects to the 4 surrounding walls, 8 screens (passive stereo projection).

4D Projection to 3D

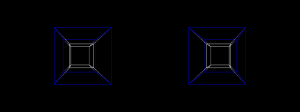
The math behind projecting 4D objects into a 3D world is very similar to the math of projecting 3D objects into the 2D world. You can choose between parallel and perspective projection. I implemented both methods (with the help of Four-Space Visualization of 4D Objects by Steven Richard Hollasch), yet came to prefer perspective projection in the setup. As in typical projection methods you need a vector for your world zero-point, a vector for your camera position and a vector for the point your camera is looking at. The perspective mode scales points according to their W-value towards the W-vanishing point (located at 0-0-0). This makes a hypercube appear as a cube with an inside cube connected to it. The inside-cube is not actually smaller, it only is depicted smaller as it is further away in the fourth dimension.

Objects

The Wand gives the user a couple of options when inside the installation. He can select his object from five different shapes.

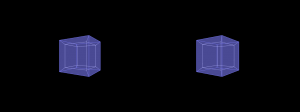
Object I -Cube
A simple 3-dimensional cube is an object everyone is familiar with and therefore a good starting point when trying to understand what happens to it, when it is rotated into the fourth dimension.

Object II - Hypercube (-1,+1)
The 4-dimensional equivalent of a cube - a hypercube. Consisting of 16 vertices, 32 edges, 24 faces, 8 cubes and 1 hyper volume. As a 3-dimensional cube is a volume covered by 6 faces, a hypercube is a hyper volume surrounded by 8 3-dimensional cubes.

Object III - Hypercube (0,+1)
This hypercube is placed between the W-dimension 0 to plus 1. By placing one of the hypercube's edges in the zero position of the fourth dimension, it is easier to relate to it as the rotation happens around the zero axis.

Object IV - Three Cubes
Three simple 3-dimensional cubes in a row shall allow you to track the spatial arrangement of objects when rotating them through 4D.

Object V - Lines
This cross of line elements was used for calibrating the system.

Display Modes

The graphics of Hyper were deliberately chosen to be very simple and abstract, as I didn't want the user to be taken in or confused by too elaborate graphics or flashy effects. The sole purpose of the project is the thought experiment.

The user can choose between different display modes. Some of them give additional information about the fourth dimension in color coding (blue = ana, white = kata), some of them are deliberately kept in one color only.

Interaction Modes

The user can choose between three different modes of interaction.

This first mode has the task to make the user comfortable in the CAVE environment. He is able to perceive the holographic effect of the object by moving around the CAVE, and adjust his eyes to the binocular disparity. With the joystick on the wand he can rotate the object around two 3-dimensional planes.

This second mode let's the user experience the fourth dimension, by giving him the option to rotate the object through 4D. He rotates the object with the joystick on the Wand around two planes that each contain the W-dimension (example: rotate around xw-plane and yw-plane). By choosing his own speed of rotation, the control to stop the rotation at any point, and the opportunity to look at the object from any angle (by stepping around it) the user can explore the fourth dimension at his own pace.

The third and advanced mode exchanges the X-axis of the physical space with the W-axis of the fourth dimension. It shall create the illusion that users are able to enter and move through the fourth dimension. By moving through the CAVE space, you now change your position in the Y-, Z- and W-axes. By stepping around the object, the user circles the object in the Z- and W-dimension (instead of X- and Z-). Every centimeter of displacement gives the user an immediate feedback in the visuals he perceives. By slowly moving around the virtual object, users should try to make sense of the spatial displacement they choose and the effect of the spatial displacement in the fourth dimension onto the representation of the object.

As an additional feature the object faces in the third mode are opaque while the user is around the 0-axis of W, and become more transparent the further he steps into the fourth dimension. A being living in the fourth dimension would be able to see the inside of 3-dimensional objects.